
Robert Wille, professor ved det tekniske universitetet i München og Software Competence Center, diskuterer nøkkelen til datastrukturer når man løser kvantedatabehandlingsproblemer
Kvantedatabehandling gjør det mulig å løse visse viktige problemer som var utenfor rekkevidde med klassiske datamaskiner. Å utvikle applikasjoner for denne nye og kommende teknologien har imidlertid vist seg å være litt av en utfordring og krever effektive verktøy. Datastrukturer er nøkkelen i denne forbindelse: Når noen har som mål å simulere, kompilere, verifisere eller feilsøke en kvantealgoritme, kreves en effektiv representasjon, f.eks. av kvantetilstander eller kvanteoperasjoner. Tatt i betraktning at disse representasjonene ofte vokser eksponentielt med hensyn til antall qubits, er dette ikke lett. I denne artikkelen gir vi en oversikt over datastrukturer for kvanteberegning tilgjengelig i dag.
Vektorer og matriser
Vektorer og matriser er de mest intuitive datastruktur for kvanteberegning. De representerer kvantetilstander og kvanteoperasjoner og kan realiseres direkte i minnet til klassiske datamaskiner gjennom 1- eller 2-dimensjonale arrays.
Denne enkle erkjennelsen kommer imidlertid med en premie: Den fører alltid til en eksponentiell mengde minne. Dette betyr at selv med enorme superdataklynger, er det maksimale antallet qubits som kan representeres med dem rundt 50 – en enorm begrensning; spesielt med tanke på det betydelige antallet qubits som fremtidige kvantedatamaskiner vil jobbe med.

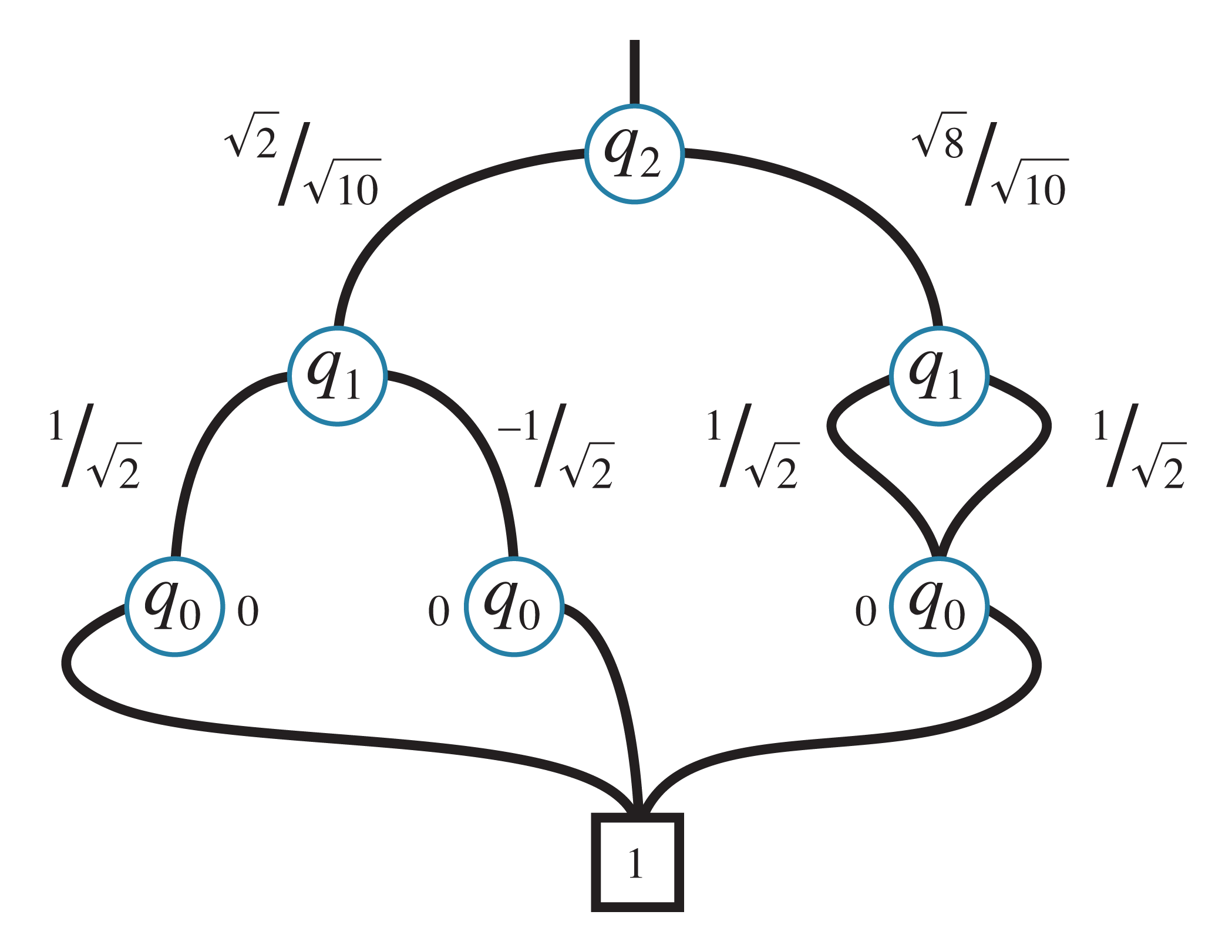
Beslutningsdiagrammer
Beslutningsdiagrammer tar sikte på å overvinne denne eksponentielle kompleksiteten ved å avdekke og utnytte redundanser innenfor de involverte kvantetilstandene og operasjonene. Den underliggende vektoren eller matrisen er representert som en graf med noder og kanter, hvor hver node tilsvarer en del av vektoren/matrisen.
Komprimeringen kommer fra deling: Identiske deler av en vektor eller en matrise (eller deler som f.eks. bare er forskjellige med en felles underfaktor) er representert av samme node. Effektiviteten av komprimeringen av beslutningsdiagrammer er svært avhengig av den betraktede kvantetilstanden eller operasjonen. Mens det er tilfeller der beslutningsdiagrammer knapt gir noen reduksjon, lar andre tilfeller krympe minnekravene fra flere terabyte til bare noen få megabyte.
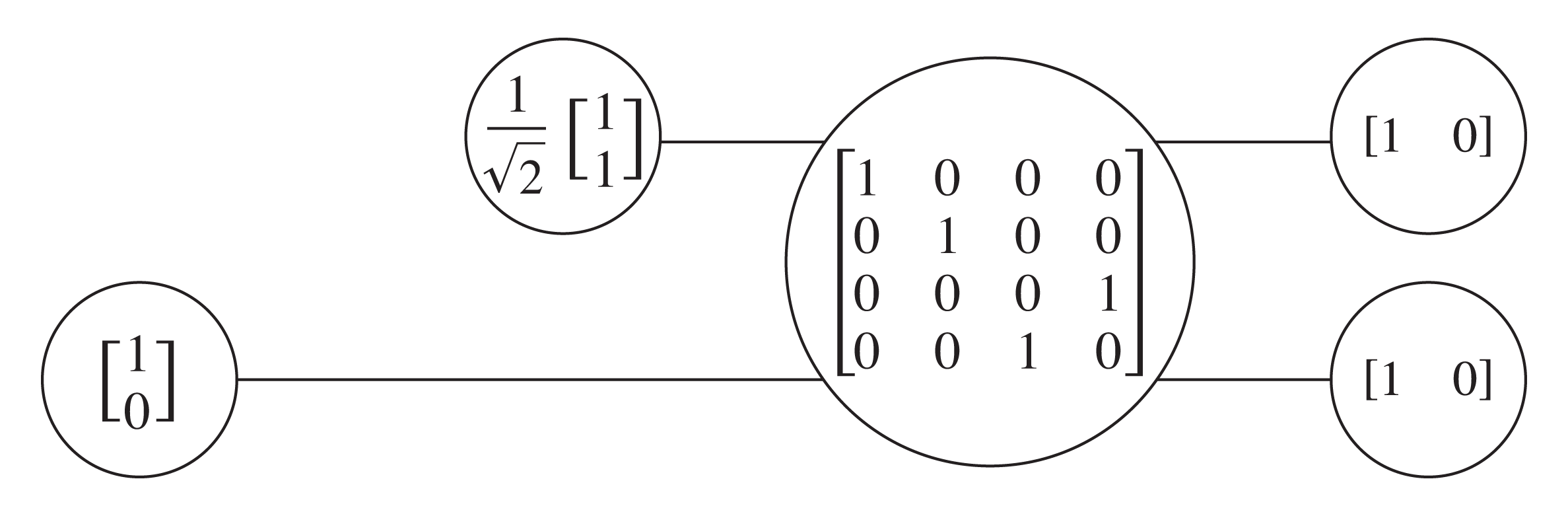
Tensor nettverk
Tensornettverk kan bidra til å lindre kompleksiteten ved å representere kvantetilstander og operasjoner ved å utnytte redundanser i den topologiske strukturen til kvantekretsen – i stedet for vektorene/matrisene. For å oversette en kvantekrets til et tensornettverk, er hvert objekt, enten det er en tilstand eller en operasjon, representert av en flerdimensjonal rekke komplekse tall – en tensor. For en krets er tensorer koblet til andre tensorer i henhold til den underliggende kvantekretsen. Deretter krever utvinning av nyttig informasjon fra et slikt tensornettverk typisk den parvise kombinasjonen av tensorer til en enkelt gjenværende tensor i en prosess som kalles sammentrekning. Å bestemme en effektiv måte å kontrahere et gitt tensornettverk på er en av hovedutfordringene, men kan til slutt føre til ganske kompakte representasjoner.
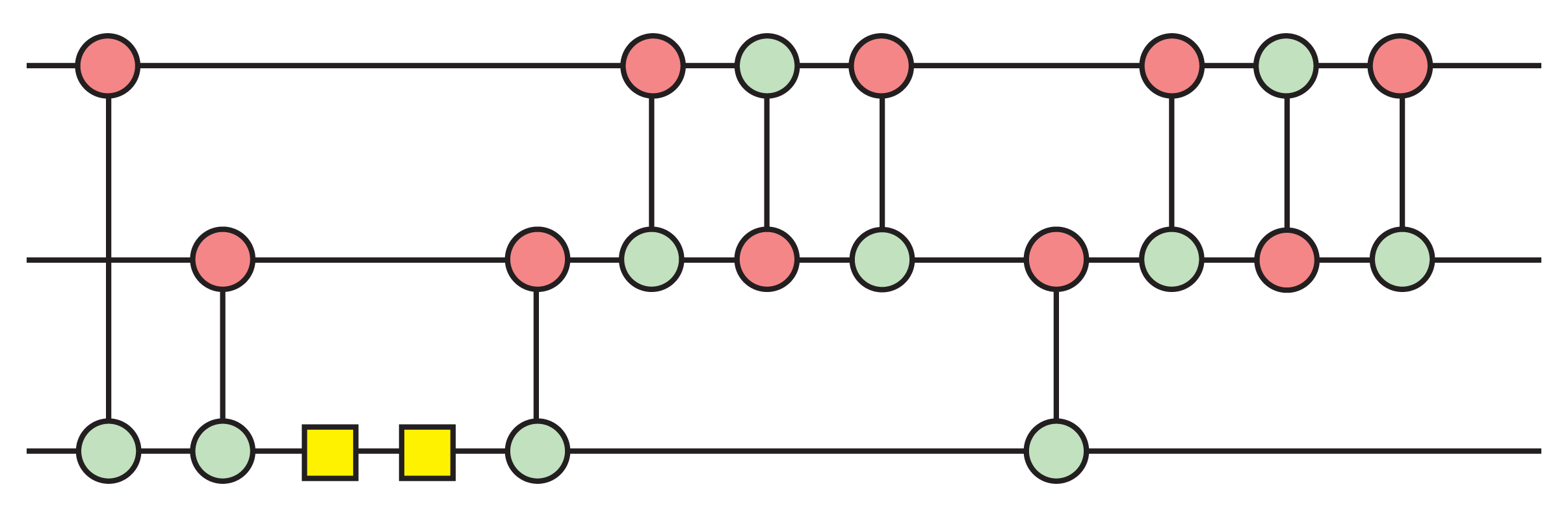
ZX-Calculus
ZX-kalkulen er en grafisk notasjon for kvantekretser utstyrt med et kraftig sett med omskrivingsregler som muliggjør diagrammatisk resonnement om kvanteberegning. Et ZX-diagram består av fargede noder (kalt edderkopper) som er forbundet med ledninger. Et viktig konsept for ZX-diagrammer er det eneste paradigmet for tilkobling, som uttrykker det faktum at to ZX-diagrammer anses som like hvis det ene kan transformeres til det andre ved å bøye ledninger.
Enhver kvantekrets kan tolkes som et ZX-diagram. ZX-diagrammer er imidlertid mer generelle enn kvantekretser, og gir rom for representasjoner som ikke har meningsfulle tolkninger som kvantekretser. Det er denne fleksibiliteten ved å kunne forlate kvantekretsformalismen som gjør ZX-kalkulen til et godt mellomspråk når man jobber med kvantekretser.
Interessert i mer?
Oversikten ovenfor gjorde deg sulten på detaljer? Deretter kan du sjekke ut følgende artikkel, som gir mer informasjon, eksplisitte eksempler og referanser for videre lesing: R. Wille, L. Burgholzer, S. Hillmich, T. Grurl, A. Ploier og T. Peham. Grunnlaget for designverktøy for kvanteberegning: arrays, beslutningsdiagrammer, tensornettverk og ZX-Calculus. In Design Automation Conference (DAC) 2022
Datastrukturene som er oppsummert ovenfor, er mye brukt i Munich Quantum Toolkit (MQT) – et programvareverktøysett for åpen kildekode for kvanteberegning utviklet ved det tekniske universitetet i München. Disse verktøyene er tilgjengelige på https://github.com/ cda-tum/.
Videre er et nettbasert grafisk grensesnitt som viser en lett visualisering av beslutningsdiagrammer for kvantekretssimulering og kvantekretsverifisering tilgjengelig på https://www.cda.cit.tum.de/app/ddvis/.
Prøv det i dag!