For å vinne i kortspillet bridge, som spilles mellom to sett med partnere, må en spiller på en eller annen måte signalisere til lagkameraten styrken på hånden de holder. Telepati ville komme godt med her. Men telepati er ikke ekte, ikke sant?
Det er riktig. I flere tiår har fysikere imidlertid mistenkt at hvis bridge ble spilt ved å bruke kort styrt av kvantemekanikkens regler, burde noe som ser uhyggelig ut som telepati være mulig. Nå har forskere i Kina eksperimentelt demonstrert denne såkalte kvantepseudotelepatien – ikke i kvantebridge, men i en kvantekonkurranse for to spillere kalt Mermin-Peres magic square (MPMS), hvor det å vinne krever at spillerne koordinerer handlingene sine uten å utveksle informasjon med hverandre. Brukt fornuftig, lar kvantepseudotelepati spillerne vinne hver eneste runde av spillet – en feilfri ytelse som ellers ville vært umulig. Eksperimentet, utført med laserfotoner, undersøker grensene for hva kvantemekanikken tillater for å tillate at informasjon deles mellom partikler.
Verket “er en vakker og enkel direkte implementering av Mermin-Peres magiske kvadratspill,” sier Arul Lakshminarayan fra Indian Institute of Technology Madras, som ikke var involvert i den eksperimentelle demonstrasjonen. Dens skjønnhet, legger han til, kommer delvis fra dens eleganse i å bekrefte at et kvantesystems tilstand ikke er godt definert før faktisk måling – noe som ofte anses for å være kvantemekanikkens mest forvirrende egenskap. “Disse kvantespillene undergraver alvorlig vår vanlige forestilling om objekter som har eksisterende egenskaper som avsløres av observasjoner,” sier han.
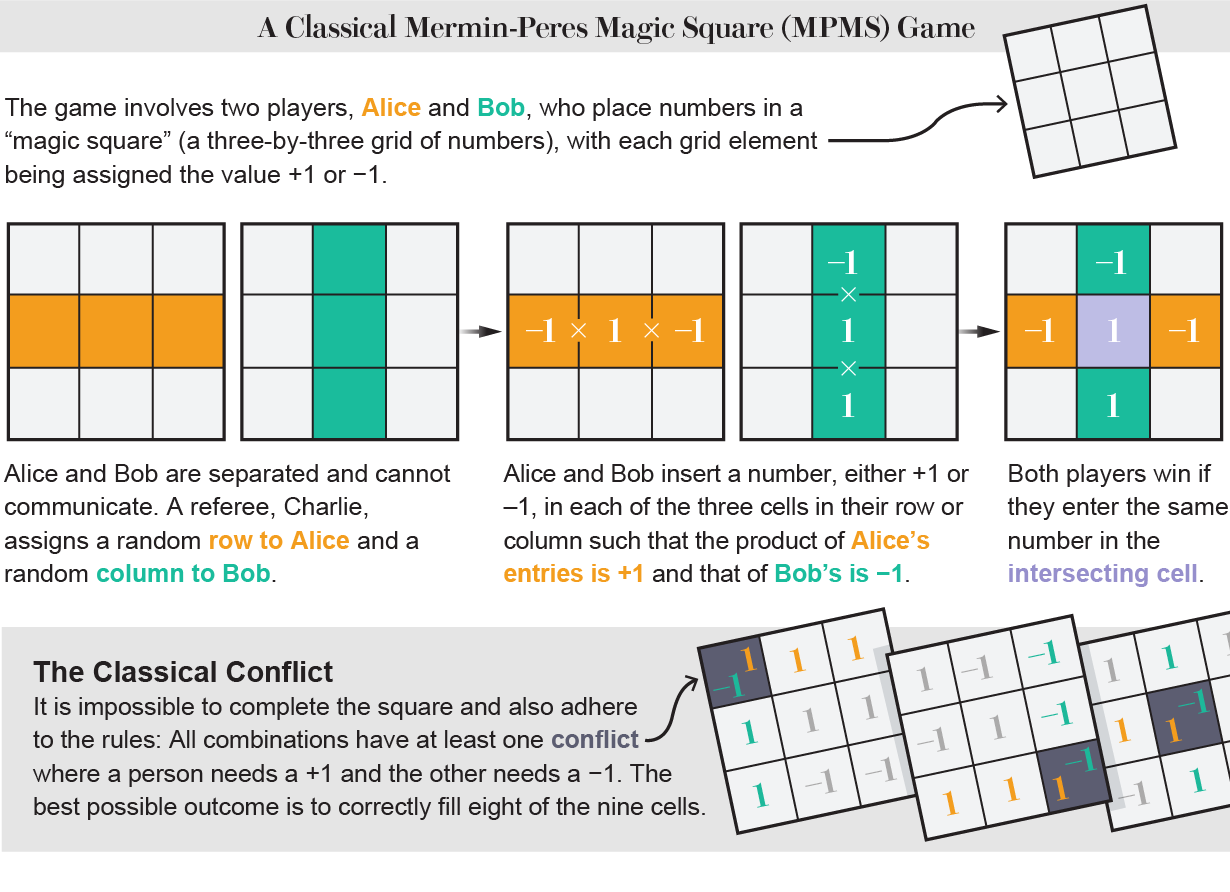
To kvantefysikere, Asher Peres og David Marmin, utviklet MPMS uavhengig i 1990. Det involverer to spillere (kalt Alice og Bob, som tradisjonen er i kvantemekaniske tankeeksperimenter) som må fylle ut en “magisk firkant” – et tre ganger tre rutenett med tall – med hvert rutenettelement blir tildelt verdien +1 eller –1. I hver runde sender en dommer (Charlie) tilfeldig en rad til Alice og deretter en kolonne til Bob (det er ni slike rad-og-kolonne-kombinasjoner). Spillerne må fortelle Charlie hvilke verdier på +1 eller –1 de skal legge inn i de tre rutenettfeltene deres. Som med enhver magisk kvadratutfordring (som Sudoku), må summene av hver rad og kolonne oppfylle spesielle begrensninger: her må produktet av alle oppføringene i en rad være lik +1, og produktet av alle kolonnene må være – 1. Alice og Bob vinner en runde hvis de begge tildeler samme verdi til rutenettelementet der kolonnen og raden overlapper hverandre.
Klassisk er det umulig å vinne alle runder, for selv om Alice og Bob gjetter godt hver gang, er det uunngåelig én runde for hver fullført rute der tildelingene deres må komme i konflikt. Det beste de kan gjøre er å oppnå åtte seire av hver ni.
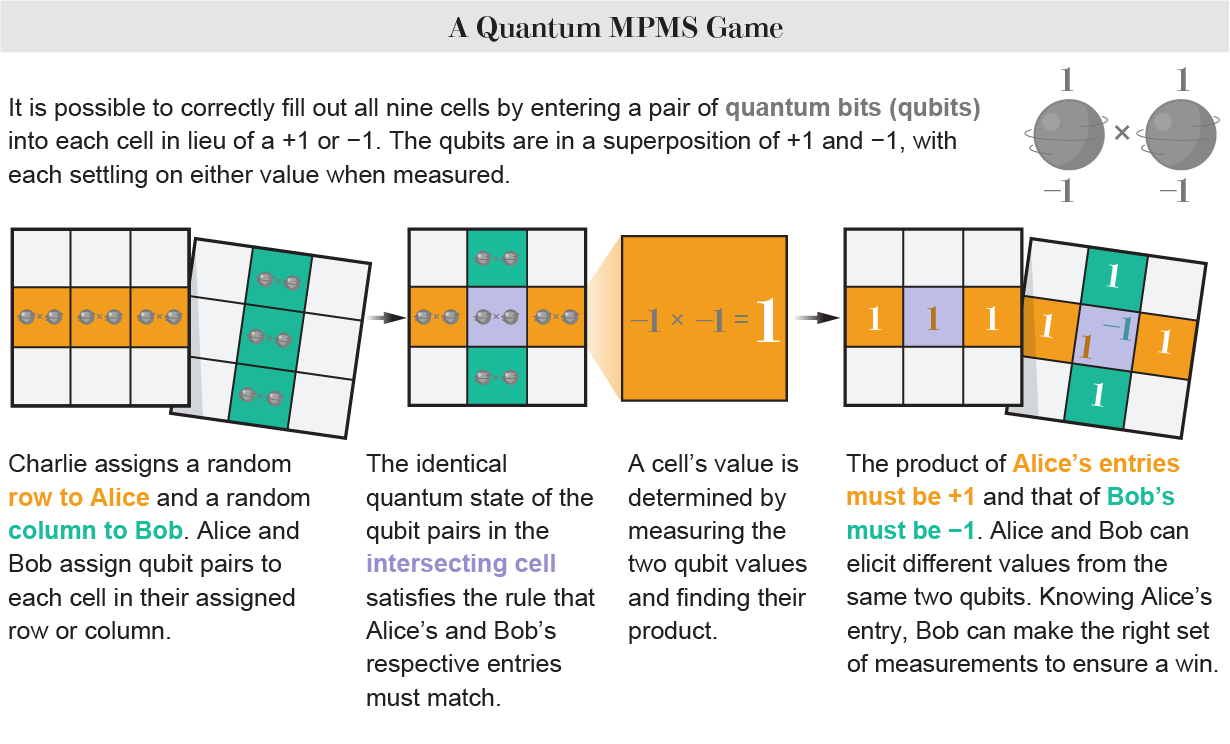
Men anta nå at Alice og Bob kan bruke denne kvantestrategien: I stedet for å tilordne hvert rutenettelement en verdi på +1 eller –1, tildeler de det et par kvantebiter (qubits), som hver har en verdi på +1 eller –1 målt. Verdien gitt av hver spiller til et bestemt rutenettelement bestemmes ved å måle de to qubit-verdiene og finne produktet av paret. Nå kan den klassiske konflikten unngås fordi Alice og Bob kan fremkalle forskjellige verdier fra de samme to qubitene avhengig av hvordan de gjør målingene sine. Det er en spesiell målestrategi som vil sikre at vinnerkriteriene for en gitt runde – at produktene til Alices og Bobs tre oppføringer er henholdsvis +1 og –1 – oppfylles for alle de ni permutasjonene av rader og kolonner.
Det er imidlertid en rynke ved denne strategien. For å gjøre det riktige settet med målinger, må Alice og Bob vite hvilket av deres tre rutenettelementer som er det som overlapper den andre spilleren – de må koordinere. Men i MPMS er dette ikke noe problem fordi de gjør målingene sekvensielt på de samme tre qubit-parene. Dette betyr at paret som når Bob har et avtrykk av hvordan Alice allerede har målt disse quibitene: de kan overføre informasjon til hverandre.
I 1993 Bullet viste at MPMS kan brukes til å demonstrere et kvantefenomen kalt kontekstualitet. Først identifisert av den nordirske fysikeren John Stewart Bell i 1966, refererer kontekstualitet til det faktum at utfallet av en kvantemåling kan avhenge av hvordan målingen gjøres. Et sett med klassiske målinger i et system vil gi de samme resultatene uansett hvilken rekkefølge disse målingene utføres i. Men for kvantemålinger er dette ikke alltid slik. I MPMS oppstår kontekstualiteten fra det faktum at målingen for et gitt qubit-par kan gi et annet resultat avhengig av hvilke to andre par som også måles.
Men hva om vi forbyr all kommunikasjon i MPMS ved å tildele Alice og Bob forskjellige qubit-par og si at de ikke kan konferere om hvordan de skal måles? Da kan hver spiller bare være garantert ni av ni seire hvis de gjør riktige gjetninger om hva den andre spilleren gjør. Men i en studie publisert i 2005, viste kvanteteoretiker Gilles Brassard fra University of Montreal og hans kolleger at spillerne kan bruke kvanteprinsipper for å garantere en seier i hver runde selv uten å kommunisere ved å bruke det de kalte kvantepseudotelepati.
Denne strategien innebærer sammenfiltring ett av hvert av de to qubit-parene sendt til Alice eller Bob med en tilsvarende qubit brukt av den andre spilleren. Sammenfiltrede partikler har egenskaper som er korrelerte, så hvis Alice måler verdien for partikkelen hennes, fikser dette verdien for Bobs partikkel også. To sammenfiltrede qubit-partikler kan være anti-relaterte, for eksempel: hvis Alices qubit er funnet å ha verdien +1, må Bobs være –1. Det er ingen måte å si hvilken verdi Alices qubit har før den måles – den kan være +1 eller –1 – men Bobs vil alltid være det motsatte. Det er viktig at en egenskap som er viklet inn mellom par av partikler, sies å være “ikke-lokal”, noe som betyr at den ikke er “lokal” for noen av partikler, men heller delt mellom begge. Selv om partiklene er atskilt med store avstander, må det sammenfiltrede paret betraktes som et enkelt, ikke-lokalt objekt. Den samme grunnleggende ideen for å vinne et kvantespill var foreslått i 2001 av kvanteteoretikeren Adán Cabello ved Universitetet i Sevilla i Spania i et spill han kalte “alt eller ingenting.” som senere ble vist å være ekvivalent med den ikke-lokale (pseudotelepatiske) MPMS.
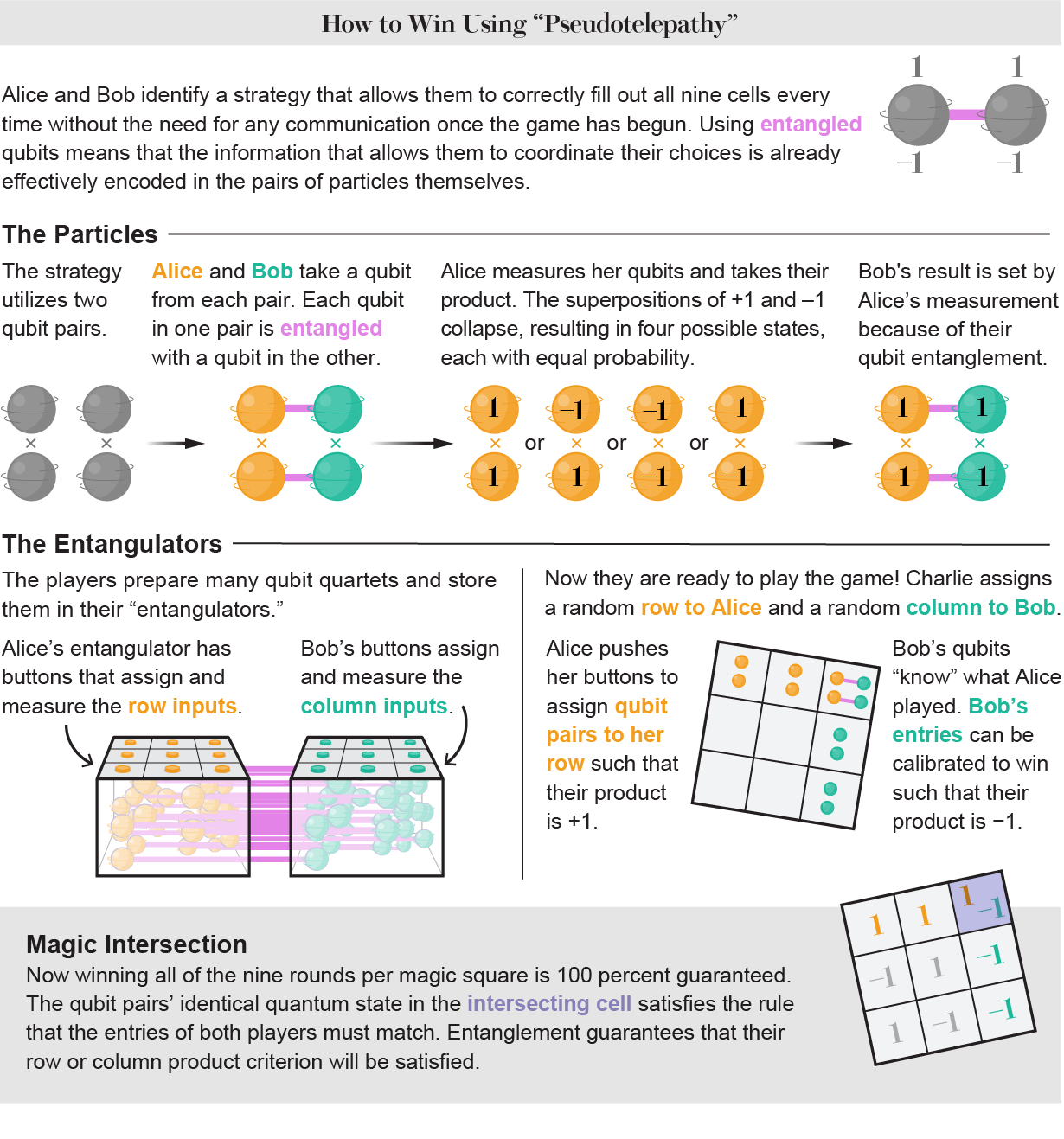
Noen forskere ser på sammenfiltring som det mest grunnleggende aspektet ved kvantemekanikk. Det innebærer en slags informasjonsdeling mellom partikler. Det er nøkkelen til å utnytte sammenfiltring for kvantepseudotelepati: Alice og Bob trenger ikke å utveksle informasjon for å koordinere sine handlinger fordi den nødvendige informasjonen allerede er delt i selve partikkelparene.
Både kontekstualitet og ikke-lokalitet gir “kvanteressurser” som kan brukes til å få en viss fordel i forhold til klassiske tilnærminger til informasjonsbehandling. I kvanteberegning, for eksempel, er sammenfiltring mellom kvantebitene generelt ressursen som skaper en snarvei til å finne en løsning på problemet som er utilgjengelig for en klassisk datamaskin.
Fysikere har gjentatte ganger demonstrert Cabellos alt-eller-ingenting-spill i den virkelige verden ved hjelp av sammenfiltrede fotoner. Men mens disse eksperimentene etablerte hvordan sammenfiltring kunne formidle en “kvantefordel” ved å slå klassisk ytelse, har Kai Chen fra University of Science and Technology i Kina, Xi-Lin Wang fra Nanjing University i Kina og deres kolleger utviklet et nytt eksperiment som de say implementerer hele protokollen for å oppnå en garantert seier i hver runde – ekte, konsekvent kvantepseudotelepati.
Ideelt sett ville Alice og Bob forberedt mange sett med fire qubits før spillet starter, hver kvartett består av to sammenfiltrede par. Alice ville få ett av hvert av disse parene, og Bob ville motta det andre. Å lage to sammenfiltrede par fotoner for hver runde av spillet er imidlertid uhyre utfordrende, sier forskerne. For det første skjer produksjonen av til og med et enkelt sammenfiltret par bare med lav sannsynlighet i apparatet deres, så å lage to samtidig vil være ekstremt usannsynlig. Og å oppdage to par på en gang, slik den pseudotelepatiske MPMS krever, er mer eller mindre umulig for denne optiske implementeringen.
I stedet forberedte Chen, Wang og deres kolleger enkeltfotonpar og sammenfiltret to av egenskapene deres uavhengig: deres polarisasjonstilstand og en egenskap kalt orbital vinkelmomentum. Fotonene var inneholdt i ultrakorte laserpulser som varte bare 150 femtosekunder og ble viklet inn ved å føre dem gjennom to såkalte ikke-lineære optiske krystaller. En tynn skive av bariumborat splittet først et enkelt foton i to fotoner med lavere energi med korrelert vinkelmoment. De ble deretter viklet inn via polarisasjonen deres, også ved å sende dem gjennom en krystall av en yttrium-vanadiumforbindelse.
For å demonstrere en nesten 100 prosent suksessrate, trengte forskerne å forbedre deteksjonseffektiviteten slik at nesten ingen av de sammenfiltrede fotonene unnslipper usett. Selv da kan den teoretiske grensen ikke nås nøyaktig i eksperimentet – men forskerne var i stand til å vise at de kunne vinne hver runde med mellom 91,5 og 97 prosent sannsynlighet. Dette betyr pålitelig å slå den klassiske åtte-av-ni-grensen i 1 009 610 runder av totalt 1 075 930 spilte.
Det pseudotelepatiske MPMS-spillet utnytter den sterkeste graden av korrelasjon mellom partikler som kvantemekanikk muligens kan gi, sier Chen. “Eksperimentet vårt undersøker hvordan man genererer ekstreme kvantekorrelasjoner mellom partikler,” sier han. Hvis disse korrelasjonene var sterkere, ville de innebære raskere enn lys informasjonsutveksling som en rekke andre uavhengige eksperimenter indikerer er umulig.
Mermin sier at selv om den er eksperimentelt imponerende, avslører ikke denne suksessen noe nytt utover det faktum at kvantemekanikk fungerer som vi trodde. Cabello er ikke helt enig. Utover det å være en eksperimentell tour de force, sier han, viser verket en ny rynke i hva kvanteregler gjør mulig ved å mobilisere to kilder til kvantefordel samtidig: en knyttet til ikke-lokalitet og den andre knyttet til kontekstualitet. Å undersøke de to effektene samtidig, sier Cabello, bør tillate fysikere å mer grundig utforske forbindelsene mellom dem.
I tillegg kan hver av disse ressursene i prinsippet brukes til forskjellig bruk i kvanteprosessering, noe som øker dens allsidighet. «For eksempel kan ikke-lokalitet brukes til hemmelig kommunikasjon [using quantum cryptography] mens kontekstualitet kan brukes til kvanteberegning, sier Cabello. I dette scenariet kunne Bob for eksempel sette opp sikker kommunikasjon med Alice samtidig som han utfører en beregning med Charlie raskere enn klassiske metoder tillater.
Bruken av delt sammenfiltring i disse eksperimentene “fører til effekter som virker klassisk magiske,” sier Lakshminarayan. Men gitt hvor ofte kvantemekanikk blir misbrukt som en falsk begrunnelse for pseudovitenskapelige påstander, ber det kanskje om problemer å kalle fenomenet “pseudotelepati”? Det er “et dårlig begrep, som inviterer til useriøse tolkninger,” sier Mermin. Men mens Cabello er enig, erkjenner han at stemningsfulle navn kan bidra til å annonsere interessen for fenomenet. “La oss ikke tulle oss selv,” sier han. «Det er sannsynligvis takket være ordet pseudotelepati som [you and I] har denne samtalen.”