
Quantum computing lover å endre måten vi takler visse problemer på i fremtiden, men utvikling av applikasjoner for denne nye og kommende teknologien har vist seg å være litt av en utfordring
Mange verktøy og bekvemmeligheter vi tar for gitt i dag når vi utvikler klassiske kretser og systemer (som simulatorer, kompilatorer, verifiseringsmetoder, debuggere eller programmeringsspråk på høyt nivå) er knapt tilgjengelig for kvanteutviklere. På grunn av dette begrenset verktøystøtte og mangel på automatisering metoder for utforming av kvanteapplikasjoner, utviklere må utføre mange av de kjedelige og feilutsatte designtrinnene manuelt. Det er anslått at utviklere for klassiske kretser og systemer allerede bruker omtrent 75 % av tiden sin på å feilsøke. Uten riktige metoder og verktøy vil dette garantert bli verre i kvanteberegning – motivere tilsvarende verifiseringstilnærminger.
Subtiliteten til feil i kvanteberegning
I motsetning til klassisk databehandling, der feil typisk manifesterer seg i form av kompilatorfeil eller programkrasj, er det feil i kvanteprogrammer ofte er mer subtile. Et kvanteprogram kan ha kjørt på en kvantedatamaskin, men de oppnådde resultatene er kanskje ikke i nærheten av det utvikleren forventet. For å gjøre saken verre, har en fersk studie vist at rundt 40 % av alle feil som oppstår ved utvikling av kvantedatabehandlingsapplikasjoner stammer fra verktøyene som brukes til utviklingen deres (f.eks. for kompilering og optimalisering). Dette betyr at når koden ikke oppfører seg som forventet, er det en 4 av 10 sjanse for at dette ikke har noe å gjøre med selve algoritmedesignet eller programmereren. Dermed kan dager og dager bli brukt på feilsøking av kode uten nytte. Det er avgjørende å gi kvanteutviklere automatiserte metoder for å sjekke at det som kjøres på kvantedatamaskinen fortsatt realiserer den opprinnelig tiltenkte funksjonaliteten.
Ekvivalenskontroll av kvantekretser
Konseptuelt er det ganske enkelt å sjekke ekvivalensen til to kvantekretser (f.eks. den algoritmiske beskrivelsen og implementeringen på lavt nivå). Funksjonaliteten til hver port g i en kvantekrets G er beskrevet av en (enhets)matrise U. Følgelig kan funksjonaliteten til en hel kvantekrets konstrueres ved å multiplisere alle individuelle portmatriser. Deretter reduseres sjekk av ekvivalensen til to kretser til sammenligningen av de respektive oppnådde matrisene. Imidlertid vokser størrelsen på de involverte matrisene eksponentielt når det gjelder antall qubits, og som et resultat nødvendiggjør det spesielle datastrukturer og metoder for alle unntatt de mest trivielle tilfellene.
Forskere ved det tekniske universitetet i München, Johannes Kepler-universitetet i Linz og Software Competence Center Hagenberg jobber med effektive teknikker for dette utfordrende problemet. I deres innsats blir beregningsparadigmet til kvanteberegning og dets tekniske egenskaper ikke sett på som en byrde, men snarere som en mulighet. I klassisk databehandling trenger ikke operasjoner å være reversible, dvs. det er ikke mulig å beregne inngangene til en operasjon fra dens utganger. For eksempel, hvis den logiske OG av a og b er 0, er det ikke mulig å bestemme a og b unikt. I kontrast er hver operasjon i kvanteberegning iboende reversibel.
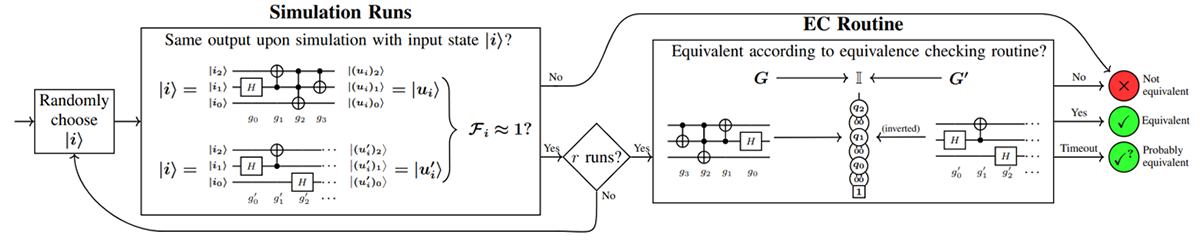
Denne reversibiliteten tillater enkelt invertere en kvantekrets (ved å reversere rekkefølgen av operasjoner og invertere hver operasjon). Ved å kombinere den opprinnelige kretsen og inversen til den andre kretsen kan man redusere spørsmålet om to kretser er ekvivalente med spørsmålet om den kombinerte kretsen realiserer identitetsfunksjonen, dvs. funksjonen der utgangen alltid er lik inngangen. For mange ofte brukte datastrukturer, som beslutningsdiagrammer eller tensornettverk, har identiteten en svært kompakt representasjon. Med utgangspunkt i denne kompakte strukturen, er en effektiv måte å sjekke om begge betraktede kretser er likeverdige å vekselvis bruke porter fra hver krets (G eller G’–1) for å holde seg så nær identiteten som mulig. Hvis identiteten resulterer på slutten av denne prosedyren, anses de aktuelle kretsene som likeverdige.
Dessuten, i klassisk databehandling, gjør det uunngåelige informasjonstapet som introduseres av mange logiske porter (slik som observert for OG-porten ovenfor) det ofte vanskelig å oppdage feil i klassiske kretser og systemer. Dermed er sofistikerte ordninger for begrensningsbasert stimuligenerering eller fuzzing nødvendig for å kontrollere funksjonaliteten til slike systemer tilstrekkelig. Igjen, kvantekarakteristikker forbedrer situasjonen betraktelig. På grunn av reversibiliteten påvirker selv små feil ofte hele funksjonaliteten til en kvantekrets. Dette gjør sondering av kvantekretser med tilfeldig valgte inngangstilstander til et gjennomførbart (og beregningsmessig mindre komplekst) alternativ til å kontrollere den fullstendige funksjonaliteten som vist ovenfor.
Et første skritt mot å hjelpe Quantum Software Engineers
Disse utfyllende observasjonene for å kontrollere ekvivalensen av kvantekretser danne en avansert ekvivalenskontrollflyt som er illustrert i figur 1. De tilsvarende metodene er publisert og innlemmet i åpen kildekode-programvare tilgjengelig for alle forskere og ingeniører på området (se boks over). Det resulterende verktøyet integreres naturlig med IBMs SDK Qiskit og kan brukes til å verifisere at en høynivå kvantekrets er riktig kompilert til en spesifikk enhet ved hjelp av Qiskit. Dette gir brukere tillit til at det som utføres på kvantedatamaskinen er det som var tiltenkt og at ingen feil har blitt introdusert gjennom kompilering.
Programvareverktøy med åpen kildekode
Verktøyene beskrevet i denne artikkelen er offentlig tilgjengelige som åpen kildekode på https://github.com/cda-tum/qcec. Videre kan du få tilgang til et nettbasert grafisk grensesnitt som viser en lett visualisering av hva som foregår under panseret til verifiseringsmetoden på https://www.cda.cit.tum.de/app/ddvis/. Flere detaljer om de skisserte konseptene er gitt på https://www.cda.cit.tum.de/research/quantum_verification/ og papirene som er koblet der.
Merk: Dette er en kommersiell profil